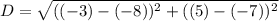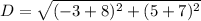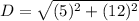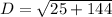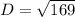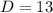Question

I need help again.lol

Answer 1

`13\ units`

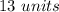
Explanation:

One is asked to find the distance between two points on a coordinate plane. The easiest way to do so is to use the distance formula, this formula is the following:

`D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2`

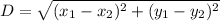
Where (
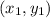`(x_1,y_1)`) and (
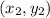`(x_2,y_2)`) are the points which one needs to find the distance between. In this case, these points are as follows:

`k\ (-3,5)`

`j\ (-8, -7)`

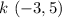
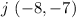
Substitute these points into the formula and solve for the distance between these points,

`D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2`

`D=\sqrt{((-3)-(-8))^2+((5)-(-7))^2`

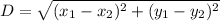
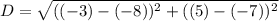
Simplify,

`D=\sqrt{((-3)-(-8))^2+((5)-(-7))^2`

`D=\sqrt{(-3+8)^2+(5+7)^2`

`D=\sqrt{(5)^2+(12)^2`

`D=√(25+144)`

`D=√(169)`

`D=13`