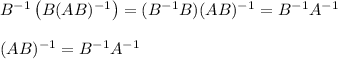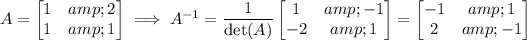
where det(A) = 1×1 - 2×1 = -1.
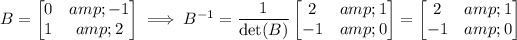
where det(B) = 0×2 - (-1)×1 = 1. Then
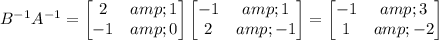
On the other side, we have
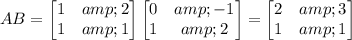
and det(AB) = det(A) det(B) = (-1)×1 = -1. So
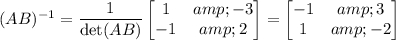
and both matrices are clearly the same.
More generally, we have by definition of inverse,
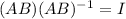
where
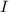 is the identity matrix. Multiply on the left by A ⁻¹ to get
is the identity matrix. Multiply on the left by A ⁻¹ to get
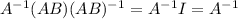
Multiplication of matrices is associative, so we can regroup terms as
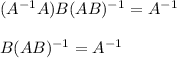
Now multiply again on the left by B ⁻¹ and do the same thing: