Question

A student answers 20 out of the first 32 questions correctly, but gets three-quarters of remaining questions wrong. all the questions are equal value. if the students' score is 40%, how many questions were there is exam?

Answer 1

80 Questions

Explanation:

First 20/32

then 3/4 questions wrong

so let's say he got there were 48 remaining questions

then he would have 36 wrong and and 12 correct

therefore it would be..

20 + 12/32 + 48

32/80

__________________________________________

so let's check the answer

it says he got 40%

so let's do 32/80

= 0.4

to convert it into percentage times by 100

= 0.4 x 100

= 40%

Answer 2

There are
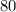`80` questions on this exam.

Explanation:

Let
`x` denote the number of questions on this exam in total (including the first
`32` questions.)

There would be
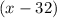`(x - 32)` questions after the first
`32`.

Since the student got three-quarters of these wrong, only one-quarter (
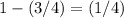`1 - (3/4) = (1/4)`) of these
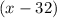`(x - 32)` questions are correct. That would be another
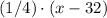`(1/4) \cdot (x - 32)` right answers.

In total, the number of questions that the student got correct would be:

`\begin{aligned} & 20 + (1)/(4) \cdot (x - 32) \\ =\; & 20 + (x)/(4) - 8 \\ =\; & 12 + (x)/(4)\end{aligned}`.

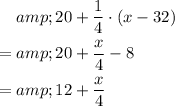On the other hand, it is given that the student got
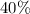`40\%` of the
`x` questions right. Hence, the number of correct answers may also be expressed as:

`\begin{aligned} & (40\%) \, x\\ =\; & (2\, x)/(5) \end{aligned}`.

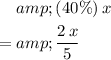Both expressions give the number of correct answers. Equate the two expressions and solve for
`x`:

`\displaystyle 12 + (x)/(4) = (2\, x)/(5)`.

`\displaystyle \left((2)/(5) - (1)/(4)\right)\, x = 12`.

`\displaystyle (8 - 5)/(20)\, x = 12`.

`\displaystyle (3)/(20)\, x = 12`.

`\begin{aligned} x &= 12 * (20)/(3) \\ &= 80\end{aligned}`.

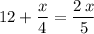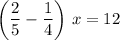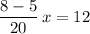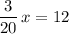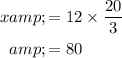In other words, there are
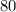`80` questions on this exam in total.