Answer:
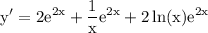
Explanation:
we would like to figure out the differential coefficient of
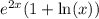
remember that,
the differential coefficient of a function y is what is now called its derivative y', therefore let,
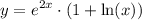
to do so distribute:
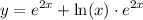
take derivative in both sides which yields:
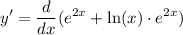
by sum derivation rule we acquire:
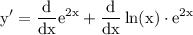
Part-A: differentiating $e^{2x}$
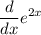
the rule of composite function derivation is given by:
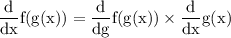
so let g(x) [2x] be u and transform it:
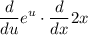
differentiate:
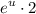
substitute back:
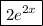
Part-B: differentiating ln(x)•e^2x
Product rule of differentiating is given by:
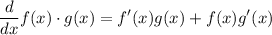
let
substitute
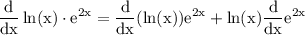
differentiate:
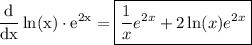
Final part:
substitute what we got:
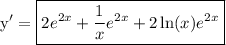
and we're done!