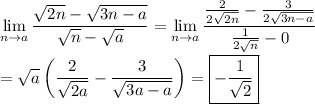Question

Needhdjdjdjdjdjdnhiskdjdjdjdjdjdjjshdjdjdjdjdjdjdjd

​

Answer 1

9514 1404 393

Answer:

-(√2)/2

Explanation:

The expression evaluated at n=a gives the indeterminate form 0/0, so L'Hopital's rule can be used to find the limit. The second expression comes from differentiating numerator and denominator. Then the form with n=a is no longer indeterminate.

`\displaystyle\lim_(n\to a){(√(2n)-√(3n-a))/(√(n)-√(a))}=\lim_(n\to a){((2)/(2√(2n))-(3)/(2√(3n-a)))/((1)/(2√(n))-0)}\\\\=√(a)\left((2)/(√(2a))-(3)/(√(3a-a))}\right)=\boxed{-(1)/(√(2))}`