Answer:
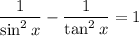
Explanation:
Prove that:
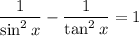
Recall that by definition:
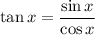
Therefore,
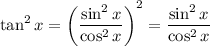
Substitute
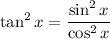 into
into
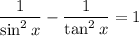 :
:
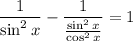
Simplify:
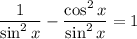
Combine like terms:
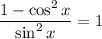
Recall the following Pythagorean Identity:
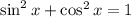 (derived from the Pythagorean Theorem)
(derived from the Pythagorean Theorem)
Subtract
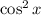 from both sides:
from both sides:
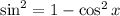
Finish by substituting
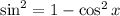 into
into
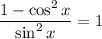 :
:
