Question

Given that tan x =3/7find cos (90-x) giving you answer in 4 significant figures​

Answer 1

`\cos \left(90 ^\circ - x\right) \approx 0.1688`

Explanation:

We are given that:

`\displaystyle \tan x = (3)/(7)`

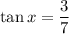
And we want to find the value of:

`\displaystyle \cos \left(90^\circ - x\right)`

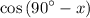
Recall that by definition, tan(θ) = sin(θ) / cos(θ). Hence:

`\displaystyle (\sin x )/(\cos x) = (3)/(7)`

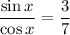
And by definition, sin(θ) = cos(90° - θ). Hence:

`\displaystyle (\cos \left(90^\circ - x\right))/(\cos x) = (3)/(7)`

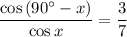
Multiply:

`\displaystyle \cos \left(90 ^\circ - x\right) = (3)/(7) \cos x`

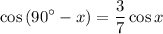
Find cosine. Recall that tangent is the ratio of the opposite side to the adjacent side. Therefore, the opposite side is 3 and the adjacent side is 7.

Thus, by the Pythagorean Theorem, the hypotenuse will be:

`\displaystyle h = √(3^2 + 7^2) = √(58)`

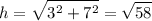
Cosine is the ratio of the adjacent side to the hypotenuse. Therefore:

`\displaystyle \cos x = (7)/(√(58))`

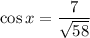
Thus:

`\displaystyle \cos \left(90 ^\circ - x\right) = (3)/(7) \left((3)/(√(58))\right)`

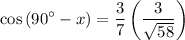
Use a calculator. Hence:

`\cos \left(90 ^\circ - x\right) \approx 0.1688`