9514 1404 393
Answer:
5i) f(x) = 3·13^x +5
5ii) f(x) = -6·(1/2)^x +5
6) f(x) = 3·8^x -1
9a) (1, 0), (0, -3)
9b) (2, 0), (0, 8)
Explanation:
5. The horizontal asymptote is y = c. To meet the requirements of the problem, you must choose c=5 and any other (non-zero) numbers for 'a' and 'b'. (You probably want 'b' to be positive, so as to avoid complex numbers.)
i) f(x) = 3·13^x +5
ii) f(x) = -6·(1/2)^x +5
__
6. You already know c=-1, so put x=0 in the equation and solve for 'a'. As in problem 5, 'b' can be any positive value.
f(0) = 2 = a·b^0 -1
3 = a
One possible function is ...
f(x) = 3·8^x -1
__
9. The x-intercept is the value of x that makes y=0. We can solve for the general case:
0 = a·b^x +c
-c = a·b^x
-c/a = b^x
Taking logarithms, we have ...
log(-c/a) = x·log(b)
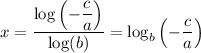
Of course, the y-intercept is (a+c), since the b-factor is 1 when x=0.
a) x-intercept: log2(6/3) = log2(2) = 1, or point (1, 0)
y-intercept: 3-6 = -3, or point (0, -3)
b) x-intercept: log3(9/1) = log3(3^2) = 2, or point (2, 0)
y-intercept: -1 +9 = 8, or point (0, 8)
_____
Additional comment
It is nice to be comfortable with logarithms. It can be helpful to remember that a logarithm is an exponent. Even so, you can solve the x-intercepts of problem 9 using the expression we had just before taking logarithms.
a) 6/3 = 2^x ⇒ 2^1 = 2^x ⇒ x=1
b) -9/-1 = 3^x ⇒ 3^2 = 3^x ⇒ x=2