Here , we need to find an formula for nth term of the sequence 26 , 35 , 44 , .....
Now , here if you notice carefully ,then you can notice that 35 - 26 = 9 , 44 - 35 = 9 , So the given sequence is an AP ( Arithmetic Progression ) with common difference being 9 , first term being 26 , so now as we knows that :
Where ,
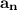 is nth term of AP ,
is nth term of AP ,
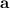 being first term while
being first term while
 is the common difference . So , now putting the values in above formula ;
is the common difference . So , now putting the values in above formula ;
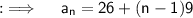

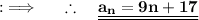
Henceforth , nth term of the sequence is 9n+17