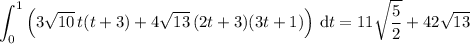Split up C into two component paths C₁ and C₂, where each line segment is respectively parameterized by
r₁(t) = (1 - t ) (3i + k) + t (4i + 3j + k) = (t + 3) i + 3t j + k
r₂(t) = (1 - t ) (4i + 3j + k) + t (4i + 5j + 4k) = 4i + (2t + 3) j + (3t + 1) k
both with 0 ≤ t ≤ 1.
It's a bit unclear what function you're supposed to integrate (looks like xyz ?) so I'll give a more general result. The line integral of a scalar function f(x, y, z) along the given path C is
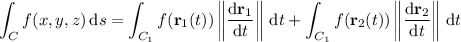
We have
dr₁/dt = i + 3j ==> || dr₁/dt || = √(1² + 3²) = √10
dr₂/dt = 2j + 3k ==> || dr₂/dt || = √(2² + 3²) = √13
Then the integrals reduce to
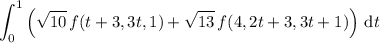
If indeed f(x, y, z) = xyz, then we have