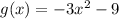Question

As above, let

$$f(x) = 3\cdot\frac{x^4+x^3+x^2+1}{x^2+x-2}.$$Give a polynomial $g(x)$ so that $f(x) + g(x)$ has a horizontal asymptote of $y=0$ as $x$ approaches positive infinity.

Answer 1

Hello,

Step-by-step explanation:

`(f(x))/(3) =(x^4+x^3+x^2+1)/((x-1)(x+2)) \\\\=((x^2+3)(x-1)(x+2)-3x+7)/((x-1)(x+2)) \\=x^2+3-(3x-7)/((x-1)(x+2)) \\\\=x^2+3-(3)/(x-1) +(1)/((x-1)(x-2)) \\\\(f(x))/(3)-(3x^2+9)/(3) =-(3)/(x-1) +(1)/((x-1)(x-2)) \\\\\\ \lim_(x \to +\infty) ((f(x))/(3)-(3x^2+9)/(3) )\\\\=0+0=0\\\\\\P(x)=-x^2-3`

Answer 2

`g(x)=-3x^2-9`

Step-by-step explanation:

`3(x^4+x^3+x^2+1)/(x^2+x-2)`

+
`(p(x)(x^2+x-2))/(x^2+x-2)`

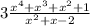
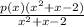
We need p(x) need to be a degree 2 polynomial so the numerator of the second fraction is degree 4. Our goal is to cancel the terms of the first fraction's numerator that are of degree 2 or higher.

So let p(x)=ax^2+bx+c.

`3(x^4+x^3+x^2+1)/(x^2+x-2)`

+
`(p(x)(x^2+x-2))/(x^2+x-2)`

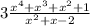
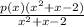
Plug in our p:

`3(x^4+x^3+x^2+1)/(x^2+x-2)`

+
`((ax^2+bx+c)(x^2+x-2))/(x^2+x-2)`

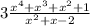
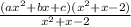
Take a break to multiply the factors of our second fraction's numerator.

Multiply:

`(ax^2+bx+c)(x^2+x-2)`

=
`ax^4+ax^3-2ax^2`

+
`bx^3+bx^2-2bx`

+
`cx^2+cx-2c`

=
`ax^4+(a+b)x^3+(-2a+b+c)x^2+(-2b+c)-2c`

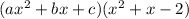
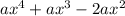
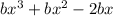
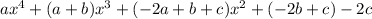
Let's go back to the problem:

`3(x^4+x^3+x^2+1)/(x^2+x-2)`

+
`(ax^4+(a+b)x^3+(-2a+b+c)x^2+(-2b+c)x-2c)/(x^2+x-2)`

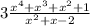
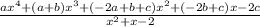
Let's distribute that 3:

`(3x^4+3x^3+2x^2+3)/(x^2+x-2)`

+
`(ax^4+(a+b)x^3+(-2a+b+c)x^2+(-2b+c)x-2c)/(x^2+x-2)[/tex</p><p></p><p>So this forces [tex]a=-3`.

Next we have
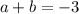`a+b=-3`. Based on previous statement this forces
`b=0`.

Next we have
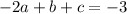`-2a+b+c=-3`. With
`b=0` and
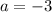`a=-3`, this gives
`6+0+c=-3`.

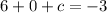So
which equals
`-2(0)+-9=-9`.

Lastly,
`-2c=-2(-9)=18`.

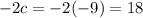This makes
`p(x)=-3x^2-9`.

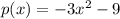This implies
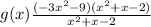`g(x)((-3x^2-9)(x^2+x-2))/(x^2+x-2)` or simplified
`g(x)=-3x^2-9`