Question

Express 0·4393939... as a fraction in its lowest term

Answer 1

`(29)/(66)`

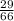
Explanation:

We require 2 equations with the repeating digits 39 placed after the decimal point.

let x = 0.43939... ( multiply both sides by 10 and 1000 )

10x = 4.3939... → (1)

1000x = 439.3939... → (2)

Subtract (1) from (2) eliminating the repeating digits

990x = 435 ( divide both sides by 990 )

x =
`(435)/(990)` =
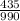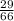`(29)/(66)` ← in simplest form

Answer 2

x= 439/999

Explanation:

let x= 0.439439.... -> eq.1

1000x= 439.439439.... -> eq.2

eq.2-eq.1 => 1000-x= 439.439....-0.439439...

999x= 439

x= 439/999