Question

Reduce the following rational expression to the lowest form


`(64x^(5) - 64x)/(( 8x^(2) +8) (2x +2) )`

please answer this. But no spam answers please
hurry

Answer 1

4x(x - 1)

Explanation:

Factor the numerator and denominator

64
`x^(5)` - 64x ← factor out 64x from both terms

= 64x(
`x^(4)` - 1) ← difference of squares

= 64x(x² - 1)(x² + 1) ← x² - 1 is also a difference of squares

= 64x(x - 1)(x + 1)(x² + 1)

---------------------------------

(8x² + 8)(2x + 2) ← factor out 8 and 2 from each factor

= 8(x² + 1) × 2(x + 1)

= 16(x² + 1)(x + 1)

Then expression can be written as

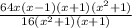`(64x(x-1)(x+1)(x^2+1))/(16(x^2+1)(x+1))` ← cancel (x² + 1) and (x + 1) on numerator/ denominator

=
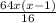`(64x(x-1))/(16)` ← cancel common factor 16 on numerator/ denominator

= 4x(x - 1)