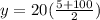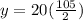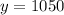5
Answer:
1050
Explanation:
Natural Numbers are positive whole numbers. They aren't negative, decimals, fractions. We can just divide 5 into 100 to find how many natural numbers go up to 100 and just add them but that is just to much.
There is a easier method.
E.g: Natural Numbers that are divisible by a Nth Number. is the same as adding the Nth Numbers to a multiple of that Nth Term. For example, let say we need to find numbers divisible by 2. We know that 4 is divisible by 2 because 4/2=2. We can add the Nth numbers which is 2 to 4. 4+2=6. And 6 is divisible by 2 because 6/2=3. We can call this a arithmetic series. A series which has a pattern of adding a common difference
Back to the problem, we can use the sum of arithmetic series formula,
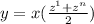
Where x is the number of terms in our sequence. Z1 is the fist term of our series. ZN is our last term. And y is the sum of all of the terms
The first term is 5, the numbers of terms being added is 20 because 100/5=20. The last term is 100.