Answer:
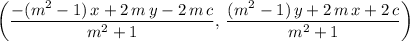 .
.
Explanation:
Consider the line that is perpendicular to
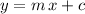 and goes through
and goes through
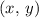 .
.
Both
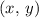 and the reflection would be on this new line. Besides, the two points would be equidistant from the intersection of this new line and line
and the reflection would be on this new line. Besides, the two points would be equidistant from the intersection of this new line and line
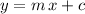 .
.
Hence, if the vector between
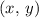 and that intersection could be found, adding twice that vector to
and that intersection could be found, adding twice that vector to
 would yield the coordinates of the reflection.
would yield the coordinates of the reflection.
Since this new line is perpendicular to line
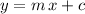 , the slope of this new line would be
, the slope of this new line would be
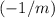 .
.
Hence,
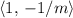 would be a direction vector of this new line.
would be a direction vector of this new line.
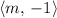 (a constant multiple of
(a constant multiple of
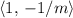 would also be a direction vector of this new line.)
would also be a direction vector of this new line.)
Both
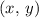 and the aforementioned intersection are on this new line. Hence, their position vectors would differ only by a constant multiple of a direction vector of this new line.
and the aforementioned intersection are on this new line. Hence, their position vectors would differ only by a constant multiple of a direction vector of this new line.
In other words, for some constant
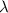 ,
,
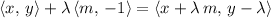 would be the position vector of the reflection of
would be the position vector of the reflection of
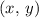 (the position vector of
(the position vector of
 is
is
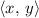 .)
.)
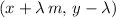 would be the coordinates of the intersection between the new line and
would be the coordinates of the intersection between the new line and
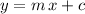 .
.
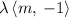 would be the vector between
would be the vector between
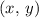 and that intersection.
and that intersection.
Since that intersection is on the line
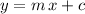 , its coordinates should satisfy:
, its coordinates should satisfy:
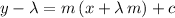 .
.
Solve for
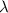 :
:
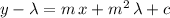 .
.
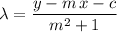 .
.
Hence, the vector between the position of
 and that of the intersection would be:
and that of the intersection would be:
 .
.
Add twice the amount of this vector to position of
 to find the position of the reflection,
to find the position of the reflection,
 .
.
 -coordinate of the reflection:
-coordinate of the reflection:
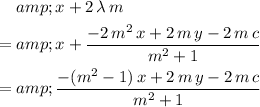 .
.
 -coordinate of the reflection:
-coordinate of the reflection:
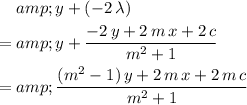 .
.