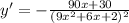Answer:
Explanation:
Never saw a problem presented in this way in all my years of teaching calculus. But I'm thinking that we need to sub that given expression for m into the equation for y and get everything into y in terms of x in order to find the derivative. I see no other way that makes sense. Can't find the derivative of y in terms of x if there's an m in there. Making that substitution:
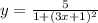 which simplifies to
which simplifies to
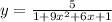 and a bit more to
and a bit more to
 and now we're ready to find the derivative. Using the quotient rule:
and now we're ready to find the derivative. Using the quotient rule:
![y'=((9x^2+6x+2)(0)-[5(18x+6)])/((9x^2+6x+2)^2)](https://img.qammunity.org/2022/formulas/mathematics/high-school/d7nm1g205v348zwub08820eog6ycw5sab9.png) which simplifies to
which simplifies to
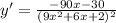 or, equally:
or, equally: