Question

A geometric series has a common ratio of (-2) and the first term is 3.

Show that the sum of the first eight positive terms of the series is 65 535.

Answer 1

see explanation

Explanation:

The sum to n terms of a geometric series is

`S_(n)` =
`(a_(1)(r^(n)-1) )/(r-1)`

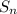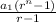
where a₁ is the first term and r the common ratio

Given a₁ = 3 and r = - 2 , then

3 × - 2 = - 6

- 6 × -2 = 12

12 × - 2 = - 24

- 24 × - 2 = 48

48 × - 2 = - 96

- 96 × - 2 = 192

The positive terms are in a geometric progression

3, 12, 48, 192, ....

with a₁ = 3 and r = 12 ÷ 3 = 48 ÷ 12 = 4 , then

S₈ =
`(3(4^(8)-1) )/(4-1)` =
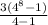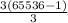`(3(65536-1))/(3)` = 65536 - 1 = 65535