Question

To find the distance AB across a river, a distance BC of 415 m is laid off on one side of the river. It is found that B = 112.2° and C = 18.3°. Find AB.

Answer 1

AB or the distance across the river is about 171.36 meters.

Explanation:

Please refer to the diagram below (not to scale). The area between the two blue lines is the river.

To find AB, we can use the Law of Sines. Recall that:

`\displaystyle (\sin A)/(a) = (\sin B)/(b) = (\sin C)/(c)`

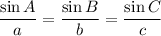
BC (or a) is opposite to ∠A and AB (or c) is opposite to ∠C. Thus, we will substitute in these values.

First, find ∠A. The interior angles of a triangle must total 180°. Thus:

`m\angle A + m\angle B + m\angle C = 180^\circ`

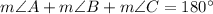
Substitute:

`\displaystyle m\angle A + (112.2^\circ) +(18.3^\circ) = 180^\circ`

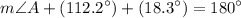
Solve for ∠A:

`m\angle A = 49.5^\circ`

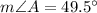
Substitute BC for a, AB for c, 49.5° for A and 18.3° for C into the Law of Sines. Thus:

`\displaystyle (\sin 49.5^\circ)/(BC) = (\sin 18.3^\circ)/(AB)`

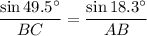
Since BC = 415 m:

`\displaystyle (\sin 49.5^\circ)/(415) = (\sin 18.3^\circ)/(AB)`

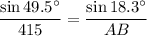
Solve for AB. Cross-multiply:

`\displaystyle AB \sin 49.5^\circ = 415\sin 18.3^\circ`

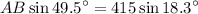
And divide:

`\displaystyle AB = (415\sin 18.3^\circ)/(\sin 49.5^\circ)`

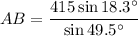
Use a calculator. Hence:

`AB = 171.3648...\approx 171.36\text{ m}`

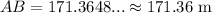
AB or the distance across the river is about 171.36 meters.