Question

An entry in the Peach Festival Poster Contest must be rectangular and have an area of 1200 square inches. Furthermore, it's length must be 20 inches longer than it's width. Find the dimensions.

Answer 1

The length is 46.05551275 inches, and the width is 26.05551275 inches.

Explanation:

We know that the area must be 1200 square inches. Using this information, we can create an equation, where x is length and y is width:

x*y=1200

We know that its length must be 20 inches longer than its width. Therefore, x=y+20. Using this new information, we can replace 'x' in 'x*y=1200' with 'y+20':

(y+20)*y=1200

`y^(2) +20y=1200`

`y^(2) +20y-1200=0`

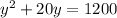
I have decided to use the quadratic formula, but you could also factor this equation into the 'intercept' form to determine the roots, which ultimately provides the same answer.

`y=\frac{-b+\sqrt{b^(2) -4ac} }{2a}`

`y=\frac{-(20)+\sqrt{(20)^(2) -4(1)(-1200)} }{2(1)}`

`y=(-(20)+√(400+4800) )/(2)`

`y=(-(20)+√(5200) )/(2)`

`y=(52.11102551 )/(2)`

`y=26.05551275` inches

`x=y+20`

`x=(26.05551275)+20`

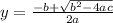
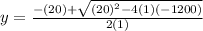
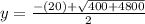
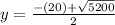
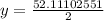
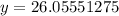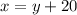
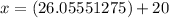
`x=46.05551275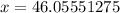` inches

Therefore, the length is 46.05551275 inches, and the width is 26.05551275 inches.