Answer:
A
Explanation:
The standard cosine function has the form:
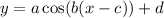
Where |a| is the amplitude, 2π / b is the period, c is the phase shift, and d is the vertical shift.
We have the function:
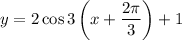
We can rewrite this as:
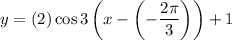
Therefore, a = 2, b = 3, c = -2π/3, and d = 1.
Our phase shift is represented by c. Thus, the phase shift is -2π/3.
Our answer is A.