Answers:
======================================================
How to get those answers:
Let w be the unknown width in centimeters. This variable is some positive real number. This means w > 0 which will be useful later.
The length is "1 cm less than 3 times its width" and it tells us the length is defined by the expression 3w-1. Whatever w is, we triple it to get 3w and then subtract 1 to get the final length.
Multiply the length and width to get the area 102
length*width = area
(3w-1)*w = 102
3w^2-w = 102
3w^2-w-102 = 0
We could guess and check our way to factoring this, but that's not very efficient. The quadratic formula is the better option. It may seem a bit messy, but it's a more direct path that doesn't involve guessing.
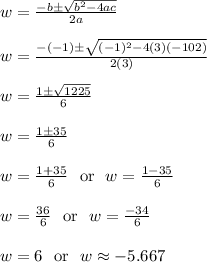
We ignore the second solution (w = -5.667 approximately) because we stated earlier that w > 0. In other words, a negative length does not make sense, so that's why we ignore it.
-----------------
If w = 6 cm is the width, then 3w-1 = 3*6-1 = 18-1 = 17 cm is the length.
Note that length*width = 17*6 = 102 which is the proper area we want. This confirms the answers.