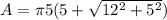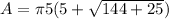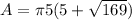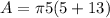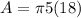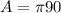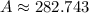Answer:
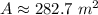
Explanation:
1. Approach
The easiest method to solve this problem is to use the Pythagorean theorem to find the height of the cone. Then one can substitute the values given and found on the cone into the formula to find the surface area in order to solve for the surface area of the given cone.
2. Height of the cone
Imagine drawing a line from the tip of the cone down to the center of the base. This line will form a right angle with the base, thus, a right triangle is formed between the line, the radius (the distance from the center to the circumference or outer edge on a circle) of the base, and the incline of the cone. The Pythagorean theorem is a formula that relates the sides of a right triangle. This formula is as follows:

Where (a) and (b) are the legs or the sides adjacent to the right angle of the right triangle, and (c) is the hypotenuse or the side opposite the right angle of the right triangle. Substitute the given values into the formula and solve for the unknown, or rather the height of the cone:

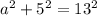
Simplify,
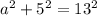
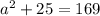
Inverse operations,
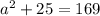
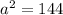
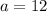
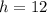
3. Find the surface area of the cone.
The following formula can be used to find the surface area of a cone:
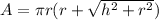
Where (
 ) represents the numerical value (3.1415...), (r) represents the radius of the base, and (h) represents the height of the cone. Substitute the given values into the formula and solve for the surface area:
) represents the numerical value (3.1415...), (r) represents the radius of the base, and (h) represents the height of the cone. Substitute the given values into the formula and solve for the surface area:
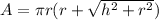
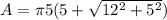
Simplify,