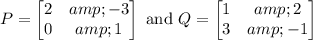Question

Please solve the problem ​

Answer 1

Explanation:

hence it has been done . check the file .

hope this helped you

any problem then comment it .

Answer 2

Treat the matrices on the right side of each equation like you would a constant.

Let 2X + Y = A and 3X - 4Y = B.

Then you can eliminate Y by taking the sum

4A + B = 4 (2X + Y) + (3X - 4Y) = 11X

==> X = (4A + B)/11

Similarly, you can eliminate X by using

-3A + 2B = -3 (2X + Y) + 2 (3X - 4Y) = -11Y

==> Y = (3A - 2B)/11

It follows that

`X=\frac4{11}\begin{bmatrix}12&-3\\10&22\end{bmatrix}+\frac1{11}\begin{bmatrix}7&-10\\-7&11\end{bmatrix} \\\\ X=\frac1{11}\left(4\begin{bmatrix}12&-3\\10&22\end{bmatrix}+\begin{bmatrix}7&-10\\-7&11\end{bmatrix}\right) \\\\ X=\frac1{11}\left(\begin{bmatrix}48&-12\\40&88\end{bmatrix}+\begin{bmatrix}7&-10\\-7&11\end{bmatrix}\right) \\\\ X=\frac1{11}\begin{bmatrix}55&-22\\33&99\end{bmatrix} \\\\ X=\begin{bmatrix}5&-2\\3&9\end{bmatrix}`

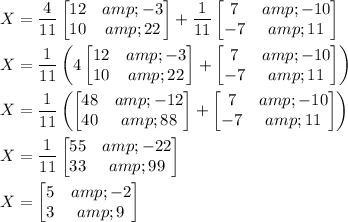
Similarly, you would find

`Y=\begin{bmatrix}2&1\\4&4\end{bmatrix}`

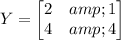
You can solve the second system in the same fashion. You would end up with

`P=\begin{bmatrix}2&-3\\0&1\end{bmatrix} \text{ and } Q=\begin{bmatrix}1&2\\3&-1\end{bmatrix}`