Answer:
Explanation:
The quadratic formula for a equation of form
ax²+bx + c = 0 is
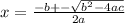
For the first equation,
x²+3x-4=0,
we can match that up with the form
ax²+bx + c = 0
to get that
ax² = x²
divide both sides by x²
a=1
3x = bx
divide both sides by x
3 = b
-4 = c
. We can match this up because no constant multiplied by x could equal x² and no constant multiplied by another constant could equal x, so corresponding terms must match up.
Plugging our values into the equation, we get
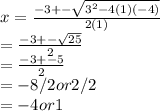
as our possible solutions
Plugging our values back into the equation, x²+3x-4=0, we see that both f(-4) and f(1) are equal to 0. Therefore, this has 2 real solutions.
Next, we have
x²+3x+4=0
Matching coefficients up, we can see that a = 1, b=3, and c=4. The quadratic equation is thus
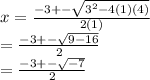
Because √-7 is not a real number, this has no real solutions. However,
(-3 + √-7)/2 and (-3 - √-7)/2 are both possible complex solutions, so this has two complex solutions
Finally, for
4x² + 1= 4x,
we can start by subtracting 4x from both sides to maintain the desired form, resulting in
4x²-4x+1=0
Then, a=4, b=-4, and c=1, making our equation
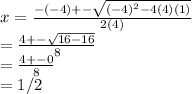
Plugging 1/2 into 4x²+1=4x, this works as the only solution. This equation has one real solution