Step-by-step explanation:
Need to FinD :
- We have to find combined velocity according to the given condition.

We know that, we're given with the mass of the boy and cart. Also, we're given the initial velocities of the two the bodies. We are asked to find out the velocity of cart after jumping of boy or just the combined velocity.
In order to find the combined velocity, we are gonna use the concept of Conservation of linear momentum. The formula for this concept is given by,
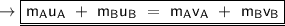
Where,
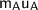 denotes the mass and the initial velocity of object one
denotes the mass and the initial velocity of object one
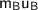 denotes the mass and the initial velocity of object two
denotes the mass and the initial velocity of object two
 denotes the mass and the final velocity of object one
denotes the mass and the final velocity of object one
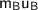 denotes the mass and the final velocity of object two
denotes the mass and the final velocity of object two
So, by substituting all the values in the formula, we'll find out the velocity of the cart after jumping of boy.



∴ Hence, the required velocity of cart after jumping of boy or the combined velocity is 19.23 ms‐¹.