Question

How many moles of Ba(OH)2 are present in 205 mL of 0.600 M Ba(OH)2?

Answer 1

Step-by-step explanation:

0.180 moles of Ba(OH)2 are present.

Answer 2

`\boxed {\boxed {\sf 0.123 \ mol \ Ba(OH)_2}}`

Step-by-step explanation:

Molarity is a measure of concentration in moles per liter. It is calculated using the following formula:

`molarity= (moles \ of \ solute)/(liters \ of \ solution)`

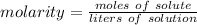
The molarity of the solution is 0.600 M Ba(OH)₂. 1 molar (M) is also equal to 1 mole per liter, so the molarity is 0.600 moles of Ba(OH)₂ per liter.

The volume of the solution is 205 milliliters, however, we need to convert the volume to liters. Remember that 1 liter contains 1000 milliliters.

• 
  `\frac { 1 \ L}{1000 \ mL}`

• 
  `205 \ mL * \frac { 1 \ L}{1000 \ mL} = \frac {205}{1000} \ L = 0.205 \ L`

Now we know the molarity and volume, but the moles are still unknown.

• molarity = 0.600 mol Ba(OH)₂/ L
• moles of solute = x
• liters of solution = 0.205 L

Substitute these values into the formula.

`0.600 \ mol \ Ba(OH)_2 /L = (x)/(0.205 \ L)`

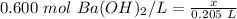
We are solving for x or the moles of solute, so we must isolate the variable. It is being divided by 0.205 liters. The inverse of division is multiplication. Multiply both sides by 0.205 L.

`0.205 \ L *0.600 \ mol \ Ba(OH)_2 /L = (x)/(0.205 \ L) * 0.205 \ L`

`0.205 \ L *0.600 \ mol \ Ba(OH)_2 /L =x`

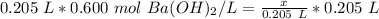
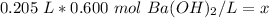
The units of liters cancel.

`0.205 *0.600 \ mol \ Ba(OH)_2 =x`

`0.123 \ mol \ Ba (OH)_2 = x`

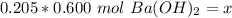
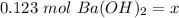
The original measurements had at least 3 significant figures. Our answer currently has 3 sig figs, so we don't need to round.

There are 0.123 moles of barium hydroxide.