Answer:
The state can issue 456,976,000 license plates.
Explanation:
For digits, it is assumed that we can use 0-9. Thus, there are 10 options for each slot with a digit.
For letters, it is assumed that we can use the 26 letters of the alphabet (i.e. A through Z). Thus, there are 26 options for each slot with a letter.
For this particular problem, the slot method can be used. Assuming that repetition of letters/digits is allowed:
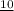
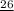
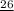
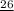
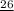
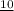
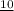
= 10*26*26*26*26*10*10
=456,976,000.
Therefore, the state can issue 456,976,000 license plates.