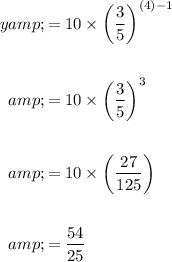Question

Work out the value of y when x = 4 30 points

Answer 1

y = 54/25 when x = 4.

Explanation:

y is given by the equation:

`\displaystyle y = p* q^(x-1)`

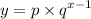
Where p and q are numbers.

We are also given that when x = 1, y = 10 and when x = 6, y = 0.7776.

And we want to determine the value of y when x = 4.

Since y = 10 when x = 1:

`\displaystyle (10) = p* q^((1)-1)`

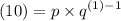
Simplify:

`10 = p * q^0`

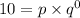
Any number (except for zero) to the zeroth power is one. Hence:

`p=10`

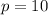
Thus, our equation is now:

`y = 10* q^(x-1)`

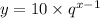
When x = 6, y = 0.7776. Thus:

`(0.7776) = 10* q^((6)-1)`

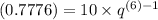
Simplify and divide both sides by ten:

`\displaystyle 0.07776 = q^5`

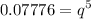
Take the fifth root of both sides:

`\displaystyle q = \sqrt[5]{0.07776}`

Use a calculator. Hence:

`\displaystyle q = (3)/(5) = 0.6`

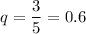
Our completed equation is:

`\displaystyle y = 10* \left((3)/(5)\right)^(x-1)`

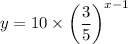
Then when x = 4, y equals:

`\displaystyle \begin{aligned} y &= 10* \left((3)/(5)\right)^((4)-1) \\ \\ &= 10* \left((3)/(5)\right)^3 \\ \\ &= 10* \left((27)/(125)\right) \\ \\ &= (54)/(25)\end{aligned}`