Question -:
The area of the rectangle whose length is
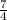 cm and breadth
cm and breadth
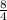 cm is ---------- cm²
cm is ---------- cm²
Explanation -:
Given -:
- Length =
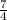 cm
cm - Breadth =
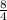 cm
cm
To Find -:
Solution -:
We know,
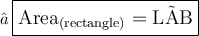
Where,
- L stand for Length
- B stand for Breadth
Substituting the values of length =
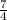 cm and breadth =
cm and breadth =
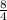 cm in the given formula
cm in the given formula
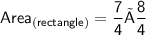

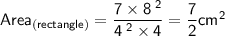
Area of the rectangle =
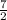 cm².
cm².
