Answer: One side could be 18 and the other side will be 33.
Explanation:
- Side #1 = 18
- Side #2 = 2x - 3
- Side #3 = x
One way of setting up the inequality is: Side #2 + Side #3 > Side #1
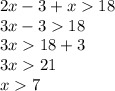
Another way of setting up the inequality is: Side #1 + Side #3 > Side #2
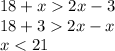
Final way of setting up the inequality is: Side #1 + Side #2 > Side #3
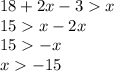
Therefore, we have the range for our value of x, which is between 7 and 21. Any possible value between works. Negative measurements are rejected. One of the sides would equal the x-value, while the other side would equal the value of 2x-3.