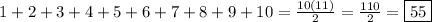Question

The telephone numbers in a small town have two digits. They run from 00 to 99.

Of the 100 possible numbers, those that become smaller when reversed are not used, i.e. 21 is not used.

What is the maximum number of telephone numbers this town could have?

Answer 1

`55`

Explanation:

We'll be using case-work to solve this problem. Let's call the ones digit of the telephone number
`B` and the tens digit
`A`. Each telephone number can be represented as
`AB`.

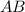Since the question states that numbers that are smaller when their digits are reversed are not used, we have the following inequality:

`B\geq A`

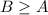
This is because if
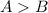`A>B`, the number would become smaller when
`A` and
`B` are switched in
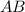`AB`. However, if
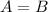`A=B` or
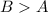`B>A`, the number will not become smaller.

Let's work our way up starting with
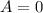`A=0`. If
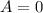`A=0`, there are 10 other numbers (0-9) that we can choose for
`B` that adhere to the condition
`B\geq A`:

`0B,\\01, 02, 03,...`

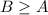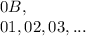
Therefore, there are 10 possible telephone numbers when the tens digit is 0.

Repeat the process, now assigning
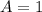`A=1`. Now, we only have the digits 1-9 to choose from for
`B`, since
`B` needs to be greater than or equal to A. Therefore, there are 9 possible telephone numbers when the tens digit is 1.

This pattern continues. As we work our way up through the cases (when increasing
`A` by 1), the number of possible telephone numbers decreases by 1, since there becomes one less option for
`B`.

The last case would be
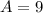`A=9` in which case there would only be one option for
`B` and that would be 9.

Since there are 10 cases (0-9), add up the possible telephone numbers for each case:

`\displaystyle \sum_(n=1)^(10)n=1+2+3+4+5+6+7+8+9+10=\boxed{55}`

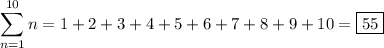
Alternatively, recall that the sum of this series can be found using
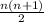`(n(n+1))/(2)`, where
`n` is the number of values in the set. In this case,
`n=10`, and we have:

`1+2+3+4+5+6+7+8+9+10=(10(11))/(2)=(110)/(2)=\boxed{55}`