Question

Please help me solve this exercise.!!

find the value of tanx if sinx+cosx=1/5 and 0<x<π.
​

Answer 1

Answer: -4/3

=============================================================

Step-by-step explanation:

Let's square both sides and do a bit of algebra to get the following.

`\sin(x) + \cos(x) = 1/5\\\\\left(\sin(x) + \cos(x)\right)^2 = \left(1/5\right)^2\\\\\sin^2(x) + 2\sin(x)\cos(x) + \cos^2(x) = 1/25\\\\\sin^2(x) + \cos^2(x) + 2\sin(x)\cos(x) = 1/25\\\\1 + 2\sin(x)\cos(x) = 1/25\\\\\sin(2x) = 1/25 - 1\\\\\sin(2x) = 1/25 - 25/25\\\\\sin(2x) = -24/25\\\\`

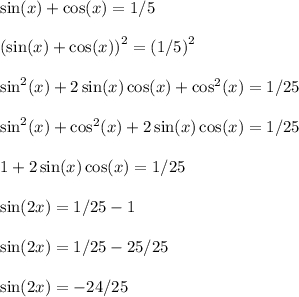
Now apply the pythagorean trig identity to determine cos(2x) based on this. You should find that cos(2x) = -7/25

This then means tan(2x) = sin(2x)/cos(2x) = 24/7.

From here, you'll use this trig identity

`\tan(2x) = (2\tan(x))/(1-\tan^2(x))\\\\`

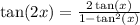
which is the same as solving

`\tan(2x) = (2w)/(1-w^2)\\\\`

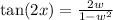
where w = tan(x)

Plug in tan(2x) = 24/7 and solve for w to get w = -4/3 or w = 3/4

So either tan(x) = -4/3 or tan(x) = 3/4.

If we were to numerically solve the original equation for x, then we'd get roughly x = 2.21; then notice how tan(2.21) = -1.345 approximately when your calculator is in radian mode.

Since tan(x) < 0 in this case, we go for tan(x) = -4/3