Question

the perimeter of a rectangular paper is 120 cm. If the breadth is 20 cm, find its length. Also find the area​

Answer 1

Explanation:

Need to FinD :

• Length of the rectangular paper.
• Area of the rectangular paper.

`\red{\frak{Given}} \begin{cases} & \sf {Perimeter\ of\ the\ rectangular\ paper\ is\ {\pmb{\sf{120\ cm}}}.} \\ &\sf {Breadth\ of\ the\ rectangular\ paper\ is\ {\pmb{\sf{20\ cm}}}.} \end{cases}`

We know that, we are given with perimeter and the breadth of the rectangular paper. And, we're asked to find out the length and the area of the rectangular paper.

• Perimeter of the rectangular paper = 120 cm.
• Breadth of the rectangular paper = 20 cm.

`{\underline{\underline{\blacksquare\ {\red{\pmb{\sf{UnderstanDing\ the\ ConcepT:}}}}}}}`

This question is from the chapter "Mensuration" which is the branch of Mathematics that deals with the computation of lengths, areas, or volumes from given dimensions or angles of a solid.

The geometric figure focused in this question are rectangle. Rectangle is a quadrilateral with four sided polygonal figure with four right angles. Also, the diagonal bisects each other.

`\begin{gathered}\begin{gathered}\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: {\huge \boxed{ \sf{ \: \: \: \: \: \: }}} \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \tiny\sf{A \: rectangle} \end{gathered}\end{gathered}`

• Perimeter = 2(l + b)
• Area = l × b

As per the analysis, we need to find out the length and area of the paper. How can we find it? We can find it by using the topic :- "Area of rectangle". To find the required answer, we've to find out the length of the paper first. And then, we will find out the area of the paper.

`\rule{200}{3}`

`{\underline{\underline{\blacksquare\ {\red{\pmb{\sf{Finding\ length\ of\ the\ paper:}}}}}}}`

`\sf \dashrightarrow {Perimeter_((rectangular\ paper))\ =\ 2(l\ +\ b)} \\ \\ \\ \sf \dashrightarrow {120\ =\ 2(l\ +\ 20)} \\ \\ \\ \sf \dashrightarrow {\frac{\cancel{120}}{\cancel{2}}\ =\ l\ +\ 20} \\ \\ \\ \sf \dashrightarrow {60\ =\ l\ +\ 20} \\ \\ \\ \sf \dashrightarrow {60\ -\ 20\ =\ l} \\ \\ \\ \sf \dashrightarrow {40\ =\ l} \\ \\ \\ \dashrightarrow {\underbrace{\boxed{\pink{\frak{Length_((rectangular\ paper))\ =\ 40\ cm}}}}_{\sf \blue{\tiny{Required\ length}}}}`

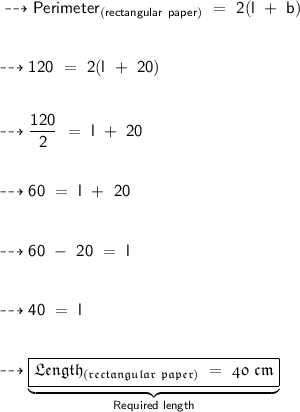
∴ Hence, the required length of the rectangular paper is 40 cm. Now, let's find out the area of the rectangular paper.

`\rule{200}{3}`

`{\underline{\underline{\blacksquare\ {\red{\pmb{\sf{Finding\ area\ of\ the\ paper:}}}}}}}`

`\sf \dashrightarrow {Area_((rectangular\ paper))\ =\ l * b} \\ \\ \\ \sf \dashrightarrow {Area_((rectangular\ paper))\ =\ 40 * 20} \\ \\ \\ \dashrightarrow {\underbrace{\boxed{\pink{\frak{Area_((rectangular\ paper))\ =\ 800\ cm^2}}}}_{\sf \blue {\tiny{Required\ area}}}}`

∴ Hence, the required area of the rectangular paper is 800 cm².