Question

I need to find the Laplace{(q'' + 110q' + 1000q)(θ(t-5))} with θ(t-a) as a Heaviside function. This is a part of a bigger problem but I don't know where to start with this part because of the notation. I am getting confused because I only know how to solve this in the form Laplace{ g(t-a)*θ(t-a) } but I don't understand how to manipulate the differential equation into that form.

Answer 1

θ(t - 5) = 1 if t ≥ 5 and 0 otherwise, so the Laplace transform of the second derivative term is

`\displaystyle \int_0^\infty q''(t) \theta(t-5) e^(-st) \, dt = \int_5^\infty q''(t) e^(-st) \, dt \\\\\\ = \int_0^\infty q''(t) e^(-st) \, dt - \int_0^5 q''(t) e^(-st) \, dt \\\\\\ = L_s\left\{q''(t)\right\} - \int_0^5 q''(t) e^(-st) \, dt`

Compute the remaining integral by parts.

`u = e^(-st) \implies du = -se^(-st) \, dt \\ dv = q''(t) \, dt \implies v = q'(t)`

`\implies \displaystyle \int_0^5 q''(t) e^(-st) \, dt = q'(t) e^(-st) \bigg|_0^5 + s \int_0^5 q'(t) e^(-st) \, dt = (q'(5))/(e^(5s)) - q'(0) + s \int_0^5 q'(t) e^(-st) \, dt`

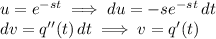
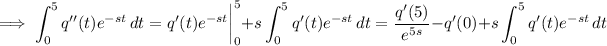
Integrating by parts again with similar choice of u and dv gives

`\displaystyle \int_0^5 q'(t) e^(-st) \, dt = (q(5))/(e^(5s)) - q(0) + s \int_0^5 q(t) e^(-st) \, dt`

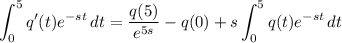
Recall that

`\displaystyle \int_0^\infty q''(t) e^(-st) \, dt = s^2 Q(s) - sq(0) - q'(0)`

`\displaystyle \int_0^\infty q'(t) e^(-st) \, dt = s Q(s) - q(0)`

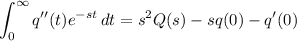
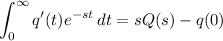
where Q(s) is the Laplace transform of q(t).

It follows that

`L_s\left\{q''(t) \theta(t-5)\right\} = (s^2 Q(s) - s q(0) - q'(0)) - \left[(q'(5))/(e^(5s)) - q'(0) + s \left((q(5))/(e^(5s)) - q(0) + s \int_0^5 q(t) e^(-st) \, dt\right) \right]`

or

`L_s\left\{q''(t) \theta(t-5)\right\} = s^2 Q(s) - (sq(5)+q'(5))/(e^(5s)) - s^2 \int_0^5 q(t) e^(-st) \, dt`

Similarly, you can show that

`L_s\left\{q'(t) \theta(t-5)\right\} = sQ(s) - (q(5))/(e^(5s)) - s\int_0^5 q(t) e^(-st) \, dt`

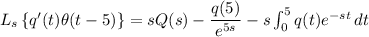
and

`L_s\left\{q(t) \theta(t-5)\right\} = Q(s) - \int_0^5 q(t) e^(-st) \, dt`

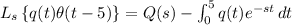
There's not much more one can say without knowing anything more about q(t) …