Answer:
 for integer
for integer
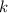 (including negative numbers.)
(including negative numbers.)
Explanation:
Pythagorean Identity:
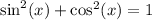 . Equivalently,
. Equivalently,
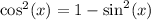 .
.
Rewrite the original equation and apply this substitution to eliminate
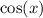 :
:
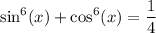 .
.
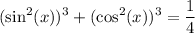 .
.
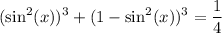 .
.
Let
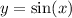 (
(
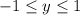 .) The original equation is equivalent to the following equation about
.) The original equation is equivalent to the following equation about
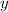 :
:
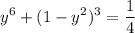 .
.
Expand the cubic binomial in the equation:
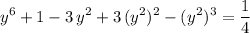 .
.
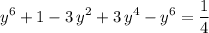 .
.
Simplify to obtain:
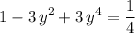 .
.
Rearrange and simplify:
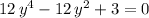 .
.
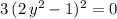 .
.
 .
.
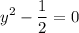 .
.
Solve for
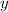 :
:
Either
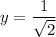 or
or
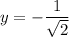 .
.
If
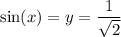 , then
, then
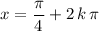 for all
for all
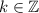 .
.
On the other hand, if
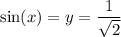 , then
, then
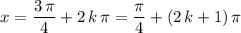 for all
for all
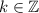 .
.
Combine both situations to obtain:
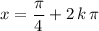 for all
for all
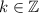 .
.