Question

Solve for x. x-6= square root of 3x​

Answer 1

`\huge\boxed{\bf\:x = 12, \:3}`

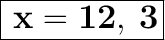
Explanation:

`x - 6 = √(3x)`

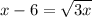
By squaring on both the sides,

`(x - 6)^(2) = (√(3x) )^(2)\\`

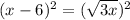
Now simplify it using the algebraic identity ⟶ (x - y)² = x² - 2xy + y². Also remember that when we square a square root the root in it will get removed.

`x^(2) - (2*x *6) + 6^(2) = 3x\\x^(2) - 12x + 36 = 3x\\x^(2) + 36 = 3x + 12x\\x^(2) + 36 = 15x`

We can change the result into the following form
`\downarrow`

`x^(2) + 36 - 15x = 0\\x^(2) - 15x + 36 = 0`

Now, this is in the standard form of a quadratic equation. Let's solve this further by using the splitting-the-middle-term method.

`x ^ { 2 } -15x+36=0\\x^(2) - 12x - 3x + 36 = 0\\x(x - 12) - 3 (x - 12) = 0\\(x - 12)(x - 3) = 0`

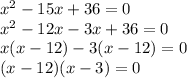
Then, the values of x are:

`(x - 12) = 0\\\boxed{x = 12}\\\\\\(x - 3) = 0\\\boxed{x = 3}`

`\rule{150}{2}`

Standard Form of a Quadratic Equation:

• ax² + bx + c = 0
• Here, a, b & c are the constants of the equation.

Splitting-the-middle-term Method:

• It's also known the factorisation or factor by grouping method.
• In this method, we need to factorise the middle term to solve the equation.

`\rule{150}{2}`