Answer:
Explanation:
The easiest way to explain this is to use slope and then writing equations for lines. The reason for that is because we are told that the production uniformly increases. That "uniform increase" is the rate of change, and since the rate of change is constant, we are talking about the slope of a line, where the rate of change is constant throughout the whole length of the line.
Create coordinates from the info given:
In the third year, 600 units were made. Time is always an x thing, so the coordinate is (3, 600). Likewise for the other bit of info. Time is always an x thing, so the coordinate is (7, 700). Applying the slope formula:
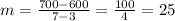 which means that 25 units per year are produced. Write the equation to find the number of units produced in any year. I used the point-slope form of a line to do this:
which means that 25 units per year are produced. Write the equation to find the number of units produced in any year. I used the point-slope form of a line to do this:
y - 600 = 25(x - 3) and
y - 600 = 25x - 75 so
y = 25x + 525
If we want to know the number of units in the first year, we will replace x with 1 and do the math:
y = 25(1) + 525 so
y = 550 units, choice C.