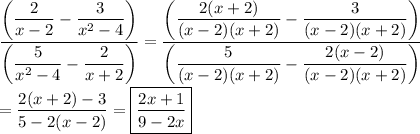9514 1404 393
Answer:
- common denominator: (x² -4)
- simplified complex fraction: (2x +1)/(9 -2x)
Explanation:
It is helpful to remember the factoring of the difference of squares:
a² -b² = (a -b)(a +b)
__
Your denominator of (x² -4) factors as (x -2)(x +2). You will note that one of these factors is the same as the denominator in the other fraction.
It looks like you want to simplify ...