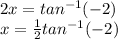Question

Help me to solve tan^3 2x-3tan2x+2=0

Answer 1

Explanation:

let tan 2x=y

y³-3y+2=0

y³-y-2y+2=0

y(y²-1)-2(y-1)=0

y(y+1)(y-1)-2(y-1)=0

(y-1)[y(y+1)-2]=0

(y-1)(y²+y-2)=0

(y-1)(y²+2y-y-2)=0

(y-1)[y(y+2)-1(y+2)]=0

(y-1)(y+2)(y-1)=0

y=1,1,-2

tan 2x=1=tanπ/4=tan (nπ+π/4)=tan π/4(n+1)

2x=π/4(n+1)

x=π/8(n+1)

where n is an integer.

tan 2x=-2

`2x=tan^(-1)(-2)\\x=(1)/(2) tan^(-1)(-2)`

Answer 2

here you are!!!!!!!!!