The question is incomplete. The complete question is :
The solid rod shown is fixed to a wall, and a torque T = 85N?m is applied to the end of the rod. The diameter of the rod is 46mm .
When the rod is circular, radial lines remain straight and sections perpendicular to the axis do not warp. In this case, the strains vary linearly along radial lines. Within the proportional limit, the stress also varies linearly along radial lines. If point A is located 12 mm from the center of the rod, what is the magnitude of the shear stress at that point?
Solution :
Given data :
Diameter of the rod : 46 mm
Torque, T = 85 Nm
The polar moment of inertia of the shaft is given by :
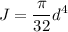
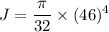
J = 207.6
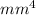
So the shear stress at point A is :
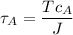
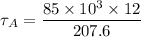
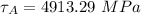
Therefore, the magnitude of the shear stress at point A is 4913.29 MPa.