Answer:

Step-by-step explanation:
We are asked to find the mass of a sample of radium-226 after half-life decay. We will use the following formula:
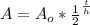
In this formula,
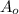 is the initial amount, t is the time, and h is the half-life.
is the initial amount, t is the time, and h is the half-life.
For this problem, the initial amount is 200 grams of radium-226, the time is 8,000 years, and the half-life is 1,600 years.
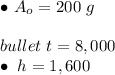
Substitute the values into the formula.
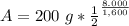
Solve the fraction in the exponent.
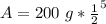
Solve the exponent.
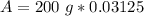
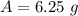
In addition, we can solve this another way. First, we find the number of half-lives by dividing the total time by the half-life.
- 8,000/1,600= 5 half-lives
Every half-life, 1/2 of the mass decays. Divide the initial mass in half, then that result in half, and so on 5 times.
- 1. 200 g/2= 100 g
- 2. 100 g / 2 = 50 g
- 3. 50 g / 2 = 25 g
- 4. 25 g / 2 = 12.5 g
- 5. 12.5 g / 6.25 g
After 8,000 years, 6.25 grams of radium-226 remains.