The question is incomplete. The complete question is :
Let
 be the density function for the shelf life of a brand of banana which lasts up to 4 weeks. Time, t, is measured in weeks and
be the density function for the shelf life of a brand of banana which lasts up to 4 weeks. Time, t, is measured in weeks and
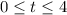 . Incorrect answer icon Your answer is incorrect. Find the mean shelf life of a banana using . Round your answer to one decimal place.
. Incorrect answer icon Your answer is incorrect. Find the mean shelf life of a banana using . Round your answer to one decimal place.
Answer:
2.4
Explanation:
Given :

Mean :

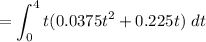
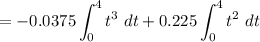
![$=-0.0375 \left[ (t^4)/(4) \right]^4_0 + 0.225 \left[ (t^3)/(3) \right]^4_0$](https://img.qammunity.org/2022/formulas/mathematics/high-school/mmwdeysykyw1qffy9gdj31e2bij8746fgu.png)
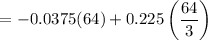

= 2.4
Therefore, the mean is 2.4