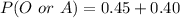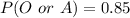Answer:
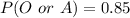
Explanation:
Given
See attachment
Required
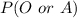
From the question, we understand that she can only get blood from O or A groups. So, the probability is represented as:
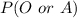
This is calculated as:
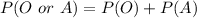
Using the American row i.e. the blood must come from an American.
We have:
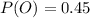
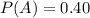
So, we have: