Answer:
Slope-intercept form:
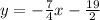
Point-slope-form:
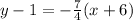
Explanation:
Hi there!
We want to find the equation of the line perpendicular to the line 4x-7y=2 that goes through (-6, 1) in slope-intercept form, as well as the point-slope form
Slope-intercept form is defined as y=mx+b, where m is the slope and b is the y intercept
Point-slope form is defined as
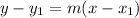 , where m is the slope and
, where m is the slope and
 is a point
is a point
Meanwhile, perpendicular lines have slopes that are negative and reciprocal. When they are multiplied together, the result is -1
So let's find the slope of the line 4x-7y=2
The equation of the line is in standard form, which is ax+by=c, where a, b, and c are integer coefficients a is non-negative, and a and b aren't 0
So let's find the slope of the line 4x-7y=2
One way to do that is to convert the equation of the line from standard form to slope-intercept form
Our goal is to isolate y onto one side
Subtract 4x from both sides
-7y=-4x+2
Divide both sides by -7
y=

So the slope of the line 4x-7y=2 is

Now, we need to find the slope of the line perpendicular to it
Use this formula:
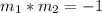
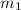 in this case is
in this case is


Multiply both sides by
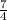
m=

Let's see the equation of the perpendicular line so far in slope-intercept form:
y=
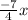 +b
+b
We need to find b now
The equation of the line passes through (-6,1), so we can use it to solve for b.
Substitute -6 as x and 1 as y

Now multiply
1=
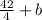
Subtract 42/4 from both sides to isolate b
-19/2=b
Substitute -19/2 as b into the equation
The equation in slope-intercept form y=
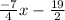
Now, here's the equation in point-slope form
Recall that the slope is
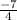 , our point is (-6, 1), and point-slope form is
, our point is (-6, 1), and point-slope form is
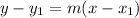
Let's label the value of everything to avoid any confusion
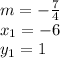
Now substitute those values into the equation
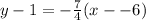
We can simplify the x--6 to x+6
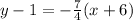
Hope this helps!