Question

What is the value of c, d, a, and b?

Answer 1

By the inscribed angle theorem, the measure of inscribed angles is half the measure of its intercepted arc, the inscribed angle measuring 100°.

Intercepts the arc measuring
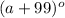`(a+99)^(o)` so:

`100=1/2(a+99)`

`200=a+99`

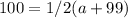
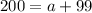
Subtract 99 from both sides

`a=101`

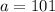
By the corollary 3 of the inscribed angle theorem, the opposite angle of a quadrilateral inscribed in a circle are supplementary so:

`c+96=180`

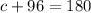
Subtract 96 from both sides

`c=84`

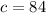
and,
`d+100=180`

`d=80`

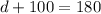
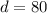
The inscribed angle measuring c° intercepts the arc measuring (a+b)° so:

`c=1/2(a+b)`

`84=1/2(101+6)`

`168=101+b`

`b=67`

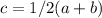
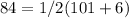
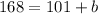
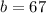
OAmalOHopeO

Answer 2

a=101

b=67

c=84

d=80

Explanation:

The measure of an intercepted arc will always be twice the measure of the inscribed angle

to find A:

2(100)=a+99

200=a+99

a=101 degrees

d=80 degrees because 100*2=200, 360-200=160, and 160/2=80

You can find c by subtracting 100, 96, and 80 from 360 and you get c=84 degrees

Find the measure of b by using what you found as measure of c and a

2(84)=101+b

168=101+b

b=67