Answer:
The answer is "(4.518, 5.182)"
Explanation:
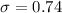
The aveage porosity for a sample of
 specimens is
specimens is
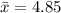
Thus, the
 confidence interval for the true mean is
confidence interval for the true mean is
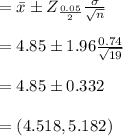
Therefore, one can state that the true average porosity will lie between 4.518 and 5.182 with the 95\% confidence.