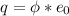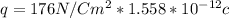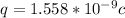Question

A cube, whose edges are aligned with the , and axes, has a side length . The field is immersed in an electric field aligned with the axis. On the left and right faces, the field has a strength and , respectively. The field along the front and back faces has strengths and . The field at the bottom and top faces has strengths and , respectively. What is the total charge enclosed by the cube

Answer 1

Complete Question

Complete Question is attached below

Answer:

`q=1.558*10^(-9)c`

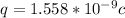
Step-by-step explanation:

From the question we are told that:

Side length s=1.13m

Left field strength
`E_l=784.75N/m`

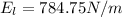
Right field strength
`E_r=776.38 N/m`

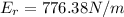
Front field strength
`E_f=725.5 N/m`

Back field strength
`E_b=749.54 N/m`

Top field strength
`E_t=944.95 N/m`

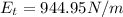
Bottom field strength
`E_(bo)=1082.58 N/m`

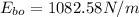
Generally, the equation for Charge flux is mathematically given by

`\phi=EAcos\theta`

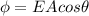
Where

Theta for Right,Left,Front and Back are at an angle 90

`cos 90=0`

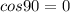
Therefore

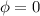`\phi =0` with respect to Right,Left,Front and Back

Generally, the equation for Charge Flux is mathematically also given by

`\phi=(q)/(e_o)`

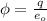
Where

`Area =L*B\\\\A=1.13*1.13\\\\A=1.2769m^2`

Therefore

`Q_(net)=E_(bo)Acos\theta_(bo) +E_tAcos\theta_t`

`Q_(net)=1082.85*1.2769*cos0=944.95*1.2769cos (180)`

`Q_(net)=176N/C m^2`

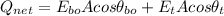
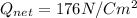
Giving

`q=\phi*e_0`

`q=176N/C m^2*1.558*10^(-12)c`

`q=1.558*10^(-9)c`