Question

The deflection plates in an oscilloscope are 10 cm by 2 cm with a gap distance of 1 mm. A 100 volt potential difference is suddenly applied to the initially uncharged plates through a 1075 ohm resistor in series with the deflection plates. How long does it take for the potential difference between the deflection plates to reach 65 volts

Answer 1

20 ns

Step-by-step explanation:

Since the deflection plates are in series with the resistor, the deflection plates act as a capacitor.

So, the set-up is a series RC circuit.

The voltage across the deflection plates V =

`V = V_(0)(1 - e^{-(t)/(RC) } )`

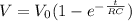
where V₀ = voltage applied = 100 V, R = resistance of resistor = 1075 Ω and C = capacitance of deflection plates and t = time to reach 65 V

The capacitance of the deflection plates C = ε₀A/d where ε₀ = permittivity of free space = 8.854 × 10⁻¹² F/m, A = area of deflection plates = 10 cm × 2 cm = 20 cm² = 20 × 10⁻⁴ m² and d = distance between deflection plates = 1 mm = 1 × 10⁻³ m.

So, C = ε₀A/d

C = 8.854 × 10⁻¹² F/m × 20 × 10⁻⁴ m²/1 × 10⁻³ m

C = 177.08 × 10⁻¹⁶ Fm/1 × 10⁻³ m

C = 177.08 × 10⁻¹³ F

C = 17.708 × 10⁻¹² F

Since we require the time it takes the capacitor to reach 65 Volts, V = 65 and we make t subject of the formula,

So,
`V = V_(0)(1 - e^{-(t)/(RC) } )`

`(V)/(V_(0)) = (1 - e^{-(t)/(RC) } )\\e^{-(t)/(RC) } = 1 - (V)/(V_(0))`

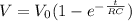
taking natural logarithm of both sides, we have

-t/RC = ㏑(1 - V/V₀)

t = -RC㏑(1 - V/V₀)

Substituting the values of the variables into the equation, we have

t = -RC㏑(1 - V/V₀)

t = -1075 Ω × 17.708 × 10⁻¹² F㏑(1 - 65 V/100 V)

t = -19036.1 × 10⁻¹² ΩF㏑(1 - 0.65)

t = -19036.1 × 10⁻¹² ΩF㏑(0.35)

t = -19036.1 × 10⁻¹² × -1.0498 s

t = 19984.5189 × 10⁻¹² s

t = 1.99845189 × 10⁻⁸ s

t = 19.99845189 × 10⁻⁹ s

t ≅ 20 × 10⁻⁹ s

t ≅ 20 ns

So, the time it takes the potential difference between the deflection plates to reach 65 V is 20 ns.