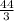Answer:
Explanation:
We'll work through this by setting up a table, as follows:
original new
width
length
It tells us the width of a rectangle is 4 feet more than the length. If we don't know the length, we'll call it L; that means that the width is L + 4, because the width is the length plus 4 more feet. Put that into column 1:
original new
width L + 4
length L
The next sentence tells us how the original rectangle is being manipulated to create a new rectangle, so that information goes into the column named "new". The original length is doubled:
original new
width L + 4
length L 2L
and the original width is decreased by 2:
original new
width L + 4 L + 4 - 2 (which simplifies to L + 2)
length L 2L
The perimeter of the new rectangle is 68. The formula for the perimeter is
P = 2L + 2w, so filling in our info along with the given perimeter:
68 = 2(L + 2) + 2(2L) and
68 = 2L + 4 + 4L and
68 = 6L + 4 and
64 = 6L so
L =
 and the width then is
and the width then is
w =
 so
so
w =