Answer:
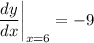
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Calculus
Differentiation
- Derivatives
- Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2022/formulas/mathematics/high-school/hrfl3gpx3dh352g7a9uj6guyxz9uxwhvl3.png)
Explanation:
Step 1: Define
Identify
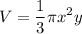
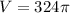
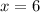
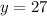
Step 2: Differentiate
- Substitute in volume [Volume Formula]:
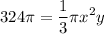
- [Equality Properties] Rewrite:
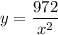
- Quotient Rule:
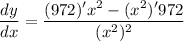
- Basic Power Rule:
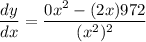
- Simplify:
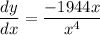
- Simplify:
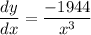
Step 3: Evaluate
- Substitute in variables [Derivative]:
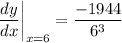
- Simplify:
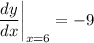
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation